ミクロな世界を支配する波、観測すると粒になりマクロな世界でみえる
はじめに
こんにちは、この世界がプログラミングされた世界だと疑っているスピリチュアル大好きみのりです。
「仮想世界を理解するための量子論①ミクロの世界とは」の記事では、量子の離散性について、波動関数、不確定性原理について触れました。
「仮想世界を理解するための量子論②二重スリット実験の罠」では、二重スリット実験、量子の観測とは、何を指し、どのように観測されるのかに迫りました。
この記事では、ミクロな世界の特徴の「おさらい」と「まとめ」を行います。
これまでに触れた波動と粒子の二重性や量子の離散性など、驚くべき性質が次第に明らかになりました。
それでは、これらの特徴を再確認し、ミクロな世界がどのように私たちの認識に問いかけを投げかけ、仮想世界にどのような影響を与えるのかを整理していきましょう。
量子の特徴の一つに、「波動と粒子の二重性」があります。 観測されるまでは波の性質を示し、観測されると粒子のように振る舞う、これが量子の基本原理です。
ミクロな粒子の観測とは、「マクロな痕跡」をつくり出すこと
通常のマクロの世界では物体や粒子は粒子として振る舞います。
対照的に、量子の世界では粒子が波動性を持ち、波の干渉や状態の共存が観測されます。
この違いを強調すると、「マクロの世界は粒子だけで、ミクロの世界は波の世界」、つまりマクロの世界では粒子、ミクロの世界では物質は波の状態と言えます。
したがって、厳密には正確な表現ではないかもしれませんが、ミクロな世界では波が支配し、その波がマクロなものと干渉して波動性を喪失し粒子に変わる瞬間、それがマクロの現象となります。
マクロなものとの干渉とは、観測器による観測のことです。
科学誌Newtonに観測とマクロな痕跡について、わかりやすく解説していたので、引用します。
量子論でいう「観測とは何か」
観測に決まった定義はありませんが、ミクロな粒子の観測とは、そのミクロな粒子が「マクロな痕跡」をつくり出すこと、と考えて良いでしょう。
マクロな痕跡とは10の何十乗個というような膨大な数の粒子に対して、元に戻すことのできない影響をあたえることです。
ミクロな粒子が観測装置を通過して、メーターの針が動いたとしたら、それはマクロの痕跡ですから、観測が行われたことになります。
メーターの針は膨大な数の原子で構成されており、ミクロな粒子はこれらに影響をあたえたわけですから、マクロな痕跡といえるわけです。
別冊Newton量子論のすべて新訂版より引用
量子の特徴を、マクロの世界と比較
わかりやすいように、量子の特徴を、マクロの世界と比較してみました。
| ミクロの世界 (例:電子や光子) | マクロの世界 (例:テニスボールやりんご) | |
|---|---|---|
| 波動と粒子の二重性 | 粒子が波動性を持ち、位置や速さが確定的でなく、波の性質が強調されます。 粒子が確定的な位置を持つ前は、波として広がっていると考えられます。 | 物体は通常、粒子として振る舞い、確定的な位置と速さを持っています。テニスボールが机の上にあれば、そこに確実にあります。 |
| 不確定性原理 (位置と運動量の同時測定) | 位置を測定するためには波動性を崩し、その結果、速さが不確定になります。逆も同様で、速さを測定すると位置が不確定になります。 | 物体の位置と速さを同時に正確に測定することが可能です。 |
| 状態の共存 (同時に複数の状態を持つ) | 粒子は同時に複数の状態を持つことができます。 これを「重ね合わせの原理」と呼び、観測が行われるまで特定の状態が確定しないと考えられます。 | 物体は通常、特定の状態にあります。 例えば、リンゴがテーブルの上にあるなら、他の場所にあることはありません。 |
| 波動関数 (波の性質を数学的に表現) | 波動関数は粒子の波動性を数学的に表現したものであり、これを用いて粒子の位置や速さを予測します。 | 物体の動きや挙動は通常の物理法則に従います。 |
| 量子の離散性 (エネルギーと物質の離散性) | エネルギーや物質の量が離散的であり、量子が特定の値を取ることが観察されます。 | エネルギーや物質の量は連続的で、無限に細かい値を取り得ます。 |
波動と粒子の二重性
量子の粒子は波としても振る舞い、同時に粒子としても存在します。これが波動と粒子の二重性であり、観測されるまで粒子の位置が不確定性を持ちます。
では、波の性質、粒子の性質とは、どのようなものをいうのでしょうか。

波の性質
波とは、振動によって伝わるエネルギーのことです。
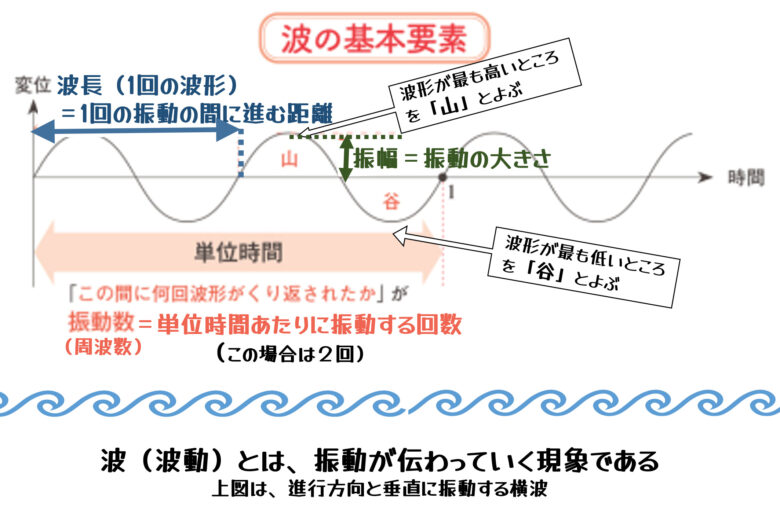
上図のように波には、振幅、波長、振動数(周波数)などの特徴があります。
- 振幅:振動の大きさ
波の振れ幅は、波が中立位置から最高点や最低点までどれだけ振れるかを示します。振幅が大きいほど、波のエネルギーも大きくなります。 - 波長:波が一周期を完了するのにかかる距離
波長が短いほど、波はより頻繁に振動し、波長が長いほど振動は疎らになります。 - 振動数(周波数):周波数は、単位時間あたりに波が振動する回数
波長と周波数は逆の関係にあり、波の速さ=波長×周波数として表現されます。
粒子の性質
粒子とは、質量と大きさを持ち、空間を占める物質のことです。
粒子には、位置、運動量などの特徴があります。
二重スリット実験と、波と粒子の二重性
二重スリット実験については、こちらの記事で「二重スリット実験でいう観測とはなにか」「観測方法」など詳しく書いていますので、省略させていただきます。
不確定性原理
波の状態=さまざまな位置に共存している、例えば、下の量子の原子模型の図でいうと、青い電子の雲のどこかにいるってことです。
つまり、どこにいるのか、わからないということです。

”電子は原子核のまわりを雲のようにおおっている。
雲は多数の電子で出来ているのではない、一つの電子がさまざまな位置に共存していることを表現したのがこの雲である。”
引用元:newton別冊「みるみる理解できる量子論」
マクロの世界では特定の位置に存在する物体も、ミクロの世界では粒子の位置は不確かであり、同時に位置と運動量(速度や運動方向)を正確に知ることはできません。
つまり、粒子の位置をより正確に知ろうとすると、運動量の測定結果はより不確かになり、逆も同様です。
これを「不確定性原理」といい、ヴェルナー・ハイゼンベルクによって提唱されたものです。
状態の共存
ミクロの世界では、粒子が複数の状態に同時に存在できるという現象。
上図でいうと、観察され、確定されるまでは、青い電子雲のすべての場所にいる可能性があることになります。
波動関数
シュレディンガーの猫でおなじみの、シュレーディンガーが考えたシュレディンガー方程式は通常、その解が波動関数と呼ばれます。
なので、シュレディンガー方程式も波動関数も量子の状態をあらわすもので同じです。
波動関数は、何かを見つける手がかりみたいなもの
波動関数のイメージを掴むために、例え話を考えました。
例えば、あなたは、部屋の中で鍵を失くしてしまったとします。
部屋のどこかには、鍵があるはずです。
そこで、部屋の中を捜し始めます。
最初は、部屋のどこにあるか、まったくわかりません。
部屋全体に鍵が落ちている可能性があります。
でも探していくと、探し終えたところは可能性から排除されていくので、鍵が落ちてる場所は絞られていきます。
このとき、鍵が落ちている可能性のある場所が、波動関数のようなものなんです。
波動関数は、鍵の存在の可能性を示しているんですね。

鍵が落ちている可能性が高い場所(まだ探していないところ)は、波動関数が大きくなっている場所。
逆に、鍵が落ちている可能性が低い場所(探し終わった場所)は、波動関数が小さくなっている場所です。
ちょっと無理があるかな…?イメージ掴めたかな?
波動関数の本質
波動関数は、量子の粒子がどのような状態にあるか、そして将来的にどのように振る舞うかを予測するものです。
つまり、ミクロな世界での量子の波の振幅を計算して、発見確率を出すものなのです。
この地点では10%、この地点では50%の確率であらわれるだろうという予測をたてるものです。
なので、マクロの世界のように、正確な場所を特定することはできません。
観測が行われると、波動関数は特定の状態に収束し、粒子の位置が確定します。
YouTube動画で、波動関数の視覚化したものを発見しましたので、リンクを貼っておきますね。
数式が理解できなくても、イメージがつかみやすいかもしれません。
udiprodチャンネル 量子物理の視覚化
波動関数の確率解釈
コペンバーゲン解釈
ミクロの世界では、波の状態の量子(粒子)ですが、観測が行われると、波動関数は収束し、粒子の位置が確定します。
この「収束する」という解釈は、コペンハーゲン解釈といわれるもので、一般向けの量子力学の書物ではこの解釈を採用しているようです。
ただ、コペンバーゲン解釈では、複数の状態が共存していたはずなのに「観測すると一つの観測しかないのはなぜか?」、「観測されなかったほかの状態は、どこへ消えたのか?」という疑問に答えていないという批判があるそうです。(右図別冊Newton量子論のすべてより引用)
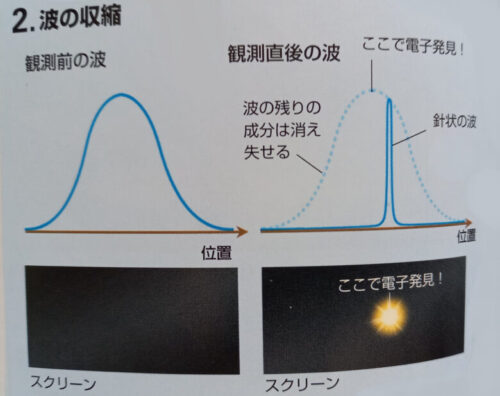
多世界解釈
観測すると波が収束して、残りは消えるというのがコペンバーゲン解釈でしたが、観測すると分岐するという多世界解釈があります。
分岐した時点でお互いの世界の関係性が切れてしまうので、たがいに影響を及ぼすことができなくなります。
並行世界とかパラレルワールドというものです。
どちらの解釈が正しいかは議論の対象であり、物理学者や研究者の間でも意見が分かれているそうです。
多世界解釈については仮想世界とも関わりがありそうだし、深堀して独自の記事にしようと考えています。
量子の離散性
量子の世界では、粒子が連続的な動きではなく、離散的な「ひとつ」「ふたつ」といった単位で動くと考えられています。
これは、量子がエネルギーや特定の物理的性質の最小単位を表しているからです。
量子の離散性については、こちらの記事で、説明していますので、ここでは省かせていただきます。